Research

(Jump to the full list of publications: New results, peer-reviewed journals, peer-reviewed conferences, non-peer-reviewed conferences, book chapters, tutorials, preprints and technical reports.)

Current Themes

Reinforcement learning

We are currently designing novel reinforcement-learning (RL) algorithms for continuous and high-dimensional state/action spaces.

We do not follow standard routes, but we introduce novel Bellman mappings which sample the state space on-the-fly, require no information on transition probabilities of Markov decision processes, and may operate with no training data available. In contrast to the prevailing line of research, which define Bellman mappings in \(\mathcal{L}_{\infty}\)-norm Banach spaces (no inner product available by definition), our Bellman mappings are designed specifically for reproducing kernel Hilbert spaces (RKHSs) to capitalize on their geometry and rich properties of their inner products.

See, for example, our papers in [IEEE Transactions on Signal Processing] and [arXiv].

We also introduce new ways to model Q-function losses via Gaussian-mixture-models and Riemannian optimization. Results on these novel directions will be reported at several publication venues.

See, for example, our preprint in (i) [arXiv] [TechRxiv].

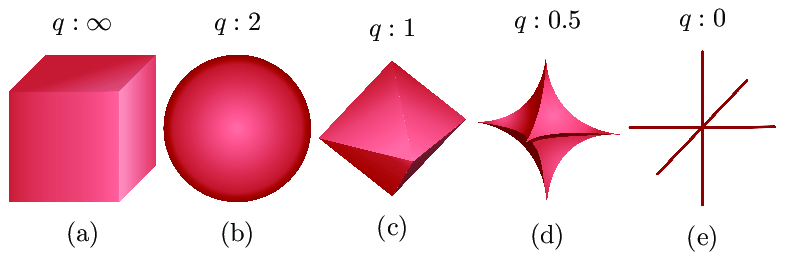
Bias reduction for sparse optimization

We study sparse optimization, which aims to estimate solutions with sparsity—vectors whose most of their entries are zero. Such sparse representation is particularly useful when only a limited subset of data or features is important, as is the case with high-dimensional data. Applications include compressive sensing, feature selection, audio and image processing, etc.

A basic problem in sparse optimization is to estimate a sparse signal/vector \(\mathbf{x}\) from measurements modeled as \(\mathbf{y} = \mathbf{Ax} + \mathbf{n}\), where \(\mathbf{n}\) is Gaussian noise. A standard approach is to minimize a cost function composed of a quadratic loss term and a sparsity-inducing penalty term. One of the most widely used methods is LASSO, which employs the \(\mathcal{L}_1\)-norm penalty. However, the \(\mathcal{L}_1\) norm is known to cause estimation bias. To address this issue, the so-called Moreau-enhancement technique has recently received significant attention. See, for example, reference 1, reference 2, and reference 3.

To this end, we proposed a robust sparse signal recovery method by exploiting an effective way of utilizing Moreau enhancement, see [IEEE Transactions on Signal Processing]. We further introduced the new notion of “external division operator,” which extends the idea of Moreau enhancement, see [IEEE ICASSP 2024]. More results on this new direction will be reported in future publications.

Regression on manifolds

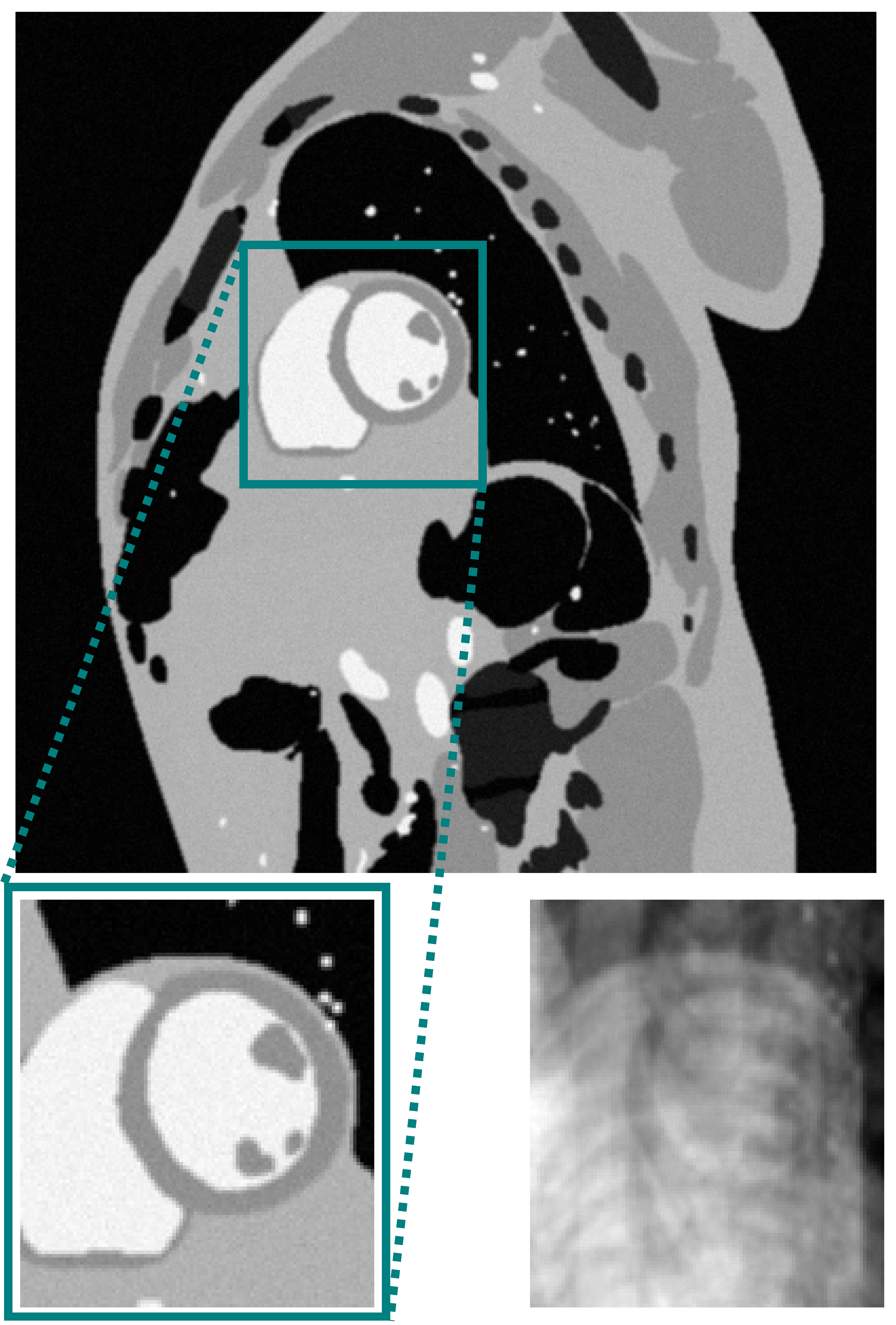
We study the problem of learning from data that live in low-dimensional manifolds.

Loosely speaking, manifolds are smooth surfaces which are usually embedded in high-dimensional spaces. Manifolds provide us a structured and rigorous way to identify latent and low-dimensional data patterns and structures.

Our preferred way of learning in this theme is regression. To this end, a novel non-parametric regression framework is introduced based only on the assumption that the underlying manifold is smooth. Neither explicit knowledge of the manifold nor training data are needed to run our regression tasks. Our design can be straightforwardly extended to reap the benefits of reproducing kernel functions; a well-known machine-learning toolbox. The framework is general enough to accommodate data with missing entries.

We validate our designs via several application domains, such as dynamic-MRI and graph signal processing where imputation of data and edge-flows in graphs is required. Several generalizations and novel research directions are currently under study.

See, for example, our papers in IEEE Open Journal of Signal Processing, IEEE Transactions on Computational Imaging, and IEEE Transactions on Medical Imaging.

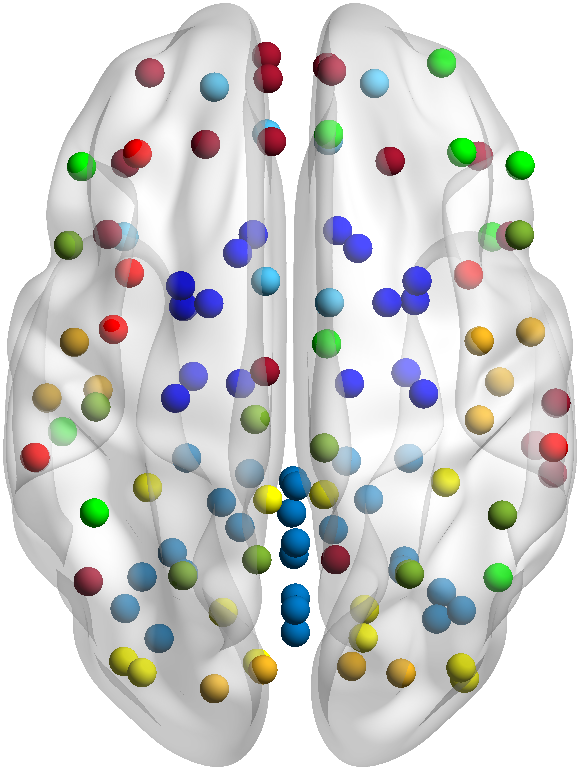
Clustering/classification on Riemannian manifolds

We study here the case of learning from data/features which live in Riemannian manifolds; a special class of manifolds endowed with an inner product and thus a distance metric.

These concepts may appear abstract, but they give us the freedom to employ our geometric intuition to address learning tasks in a wide variety of application domains. For example, numerous well-known features in signal processing and machine learning belong to Riemannian manifolds; see correlation matrices, orthogonal matrices, fixed-rank linear subspaces and tensors, probability density functions, etc.

With regards to applications, we consider the basic learning tasks of clustering and classification on data taken from network time series, and in particular, from brain networks. Several research directions are currently under study.

See, for example, our papers in IEEE Open Journal of Signal Processing and Signal Processing.

Quantum signal processing and machine learning

Several directions are currently under study, and results will be reported soon via journal/conference publications.






Full List of Publications

New results

  1. Y. Akiyama and K. Slavakis. Nonparametric Bellman mappings for value iteration in distributed reinforcement learning. 2025. [arXiv]

  2. D. T. Nguyen, K. Slavakis, and D. Pados. Imputation of time-varying edge flows in graphs by multilinear kernel regression and manifold learning. 2024. [arXiv] [TechRxiv]

  3. M. Vu and K. Slavakis. Gaussian-mixture-model Q-functions for reinforcement learning by Riemannian optimization. 2024. [arXiv] [TechRxiv]

Peer-reviewed journals

  1. D. S. Wack, F. Schweser, A. S. Wack, S. F. Muldoon, K. Slavakis, C. McGranor, E. Kelly, R. Miletich, and K. McNerney. Speech in noise listening correlates identified in resting state and DTI MRI images. Brain and Language, vol. 260, January 2025.

  2. Y. Akiyama, M. Vu, and K. Slavakis. Nonparametric Bellman mappings for reinforcement learning: Application to robust adaptive filtering. IEEE Transactions on Signal Processing, vol. 72, pp. 5644-5658, 2024.

    (Missing qualifiers of Q from Proposition 1 of the published paper have been corrected here.)

  3. D. T. Nguyen and K. Slavakis. Multilinear kernel regression and imputation via manifold learning. IEEE Open Journal of Signal Processing, vol. 5, pp. 1073-1088, 2024.

  4. Y. Chen, K. Okubo, K. Slavakis, and Y. Kitamoto. Estimation of biomolecule amount by analyzing magnetic nanoparticle cluster distributions from alternating current magnetization spectra for magnetic biosensing. Journal of Magnetism and Magnetic Materials, vol. 588, part A, pp. 171387, December 2023.

  5. K. Slavakis, G. N. Shetty, L. Cannelli, G. Scutari, U. Nakarmi, and L. Ying. Kernel regression imputation in manifolds via bi-linear modeling: The dynamic-MRI case. IEEE Transactions on Computational Imaging, vol. 8, pp. 133-147, 2022. [Julia code for the numerical tests: GitHub.]

  6. C. Ye, K. Slavakis, J. Nakuci, S. F. Muldoon, and J. Medaglia. Fast sequential clustering in Riemannian manifolds for dynamic and time-series-annotated multilayer networks. IEEE Open Journal of Signal Processing, vol. 2, pp. 67-84, 2021.

  7. C. Ye, K. Slavakis, P. V. Patil, J. Nakuci, S. F. Muldoon, and J. Medaglia. Network clustering via kernel-ARMA modeling and the Grassmannian: The brain-network case. Signal Processing, vol. 179, pp. 107834, February 2021.

  8. G. N. Shetty, K. Slavakis, A. Bose, U. Nakarmi, G. Scutari, and L. Ying. Bi-linear modeling of data manifolds for dynamic-MRI recovery. IEEE Transactions on Medical Imaging, vol. 39, no. 3, pp. 688-702, March 2020.

  9. K. Slavakis and S. Banerjee. Robust hierarchical-optimization RLS against sparse outliers. IEEE Signal Processing Letters, vol. 27, pp. 171-175, 2020. [Julia code for the numerical tests: GitHub.]

  10. K. Slavakis. The stochastic Fejér-monotone hybrid steepest descent method and the hierarchical RLS. IEEE Transactions on Signal Processing, vol. 67, no. 11, pp. 2868-2883, June 2019. [Matlab code for the numerical tests: GitHub.]

  11. K. Slavakis and I. Yamada. Fejér-monotone hybrid steepest descent method for affinely constrained and composite convex minimization tasks. Optimization, vol. 67, no. 11, pp. 1963-2001, 2018. [arXiv]

  12. K. Slavakis, S. Salsabilian, D. S. Wack, S. F. Muldoon, H. E. Baidoo-Williams, J. M. Vettel, M. Cieslak and S. T. Grafton. Clustering brain-network time series by Riemannian geometry. IEEE Transactions on Signal and Information Processing over Networks, vol. 4, no. 3, pp. 519-533, Sept. 2018.

  13. P. A. Traganitis, K. Slavakis and G. B. Giannakis. Sketch and validate for big data clustering. IEEE Journal of Selected Topics in Signal Processing, vol. 9, no. 4, pp. 678-690, June 2015.

  14. K. Slavakis, S.-J. Kim, G. Mateos and G. B. Giannakis. Stochastic approximation vis-a-vis online learning for big data analytics. IEEE Signal Processing Magazine, vol. 31, no. 6, pp. 124-129, Nov. 2014.

  15. K. Slavakis, G. B. Giannakis and G. Mateos. Modeling and optimization for big data analytics. IEEE Signal Processing Magazine, vol. 31, no. 5, pp. 18-31, Sept. 2014.

  16. K. Slavakis, Y. Kopsinis, S. Theodoridis and S. McLaughlin. Generalized thresholding and online sparsity-aware learning in a union of subspaces. IEEE Transactions on Signal Processing, vol. 61, no. 15, pp. 3760-3773, 2013.

  17. S. Chouvardas, K. Slavakis, S. Theodoridis and I. Yamada. Stochastic analysis of hyperslab-based adaptive projected subgradient method under bounded noise. IEEE Signal Processing Letters, vol. 20, no. 7, pp. 729-732, 2013</font>.

  18. S. Chouvardas, K. Slavakis and S. Theodoridis. Trading off complexity with communication costs in distributed adaptive learning via Krylov subspaces for dimensionality reduction. IEEE Journal of Selected Topics in Signal Processing, vol. 7, no. 2, pp. 257-273, April 2013.

  19. K. Slavakis and I. Yamada. The adaptive projected subgradient method constrained by families of quasi-nonexpansive mappings and its application to online learning. SIAM Journal on Optimization, vol. 23, no. 1, pp. 126-152, 2013.

  20. S. Chouvardas, K. Slavakis, Y. Kopsinis and S. Theodoridis. A sparsity promoting adaptive algorithm for distributed learning. IEEE Transactions on Signal Processing, vol. 60, no. 10, pp. 5412-5425, Oct. 2012.

  21. P. Bouboulis, K. Slavakis and S. Theodoridis. Adaptive learning in complex reproducing kernel Hilbert spaces employing Wirtinger's subgradients. IEEE Transactions on Neural Networks and Learning Systems, vol. 23, no. 3, pp. 425-438, Mar. 2012.

  22. K. Slavakis, P. Bouboulis and S. Theodoridis. Adaptive multiregression in reproducing kernel Hilbert spaces: The multiaccess MIMO channel case. IEEE Transactions on Neural Networks and Learning Systems, vol. 23, no. 2, pp. 260-276, Feb. 2012.

  23. S. Chouvardas, K. Slavakis and S. Theodoridis. Adaptive robust distributed learning in diffusion sensor networks. IEEE Transactions on Signal Processing, vol. 59, no. 10, pp. 4692-4707, Oct. 2011.

  24. Y. Kopsinis, K. Slavakis and S. Theodoridis. Online sparse system identification and signal reconstruction using projections onto weighted l1 balls. IEEE Transactions on Signal Processing, vol. 59, no. 3, pp. 936-952, March 2011.

  25. S. Theodoridis, K. Slavakis and I. Yamada. Adaptive learning in a world of projections: A unifying framework for linear and nonlinear classification and regression tasks. IEEE Signal Processing Magazine, vol. 28, no. 1, pp. 97-123, January 2011 (2014 IEEE Signal Processing Magazine best-paper award).

  26. P. Bouboulis, K. Slavakis and S. Theodoridis. Adaptive kernel-based image denoising employing semi-parametric regularization. IEEE Transactions on Image Processing, vol. 19, no. 6, pp. 1465-1479, June 2010.

  27. A. Georgiadis and K. Slavakis. Stability optimization of the coupled oscillator array steady state solution. IEEE Transactions on Antennas & Propagation, vol. 58, no. 2, pp. 608-612, Feb. 2010.

  28. M. Yukawa, K. Slavakis and I. Yamada. Multi-domain adaptive learning based on feasibility splitting and adaptive projected subgradient method. IEICE Transactions on Fundamentals, E93-A (2): 456-466, Feb. 2010.

  29. K. Slavakis, S. Theodoridis and I. Yamada. Adaptive constrained learning in reproducing kernel Hilbert spaces: The robust beamforming case. IEEE Transactions on Signal Processing, 57 (12): 4744-4764, Dec. 2009.

  30. K. Slavakis, S. Theodoridis and I. Yamada. Online kernel-based classification using adaptive projection algorithms. IEEE Transactions on Signal Processing, 56 (7), Part 1: 2781-2796, July 2008.

  31. K. Slavakis and S. Theodoridis. Sliding window generalized kernel affine projection algorithm using projection mappings, EURASIP Journal on Advances in Signal Processing, Special Issue: Emerging Machine Learning Techniques in Signal Processing, vol. 2008, 16 pages, 2008.

  32. A. Georgiadis and K. Slavakis. A convex optimization method for constrained beam-steering in planar (2-D) coupled oscillator antenna arrays. IEEE Transactions on Antennas and Propagation, 55 (10): 2925-2928, October 2007.

  33. K. Slavakis and I. Yamada. Robust wideband beamforming by the hybrid steepest descent method. IEEE Transactions on Signal Processing, 55 (9): 4511-4522, September 2007.

  34. M. Yukawa, K. Slavakis and I. Yamada. Adaptive parallel quadratic-metric projection algorithms. IEEE Transactions on Audio, Speech, and Signal Processing, 15 (5): 1665-1680, July 2007.

  35. K. Slavakis, I. Yamada, and N. Ogura. The adaptive projected subgradient method over the fixed point set of strongly attracting nonexpansive mappings. Numerical Functional Analysis and Optimization, 27 (7&8): 905-930, November 2006.

  36. K. Slavakis, I. Yamada, and K. Sakaniwa. Computation of symmetric positive definite Toeplitz matrices by the hybrid steepest descent method. Signal Processing, 83: 1135-1140, 2003.

  37. I. Yamada, K. Slavakis, and K. Yamada. An efficient robust adaptive filtering algorithm based on parallel subgradient projection techniques. IEEE Transactions on Signal Processing, 50 (5): 1091-1101, May 2002.

  38. K. Slavakis and I. Yamada. Biorthogonal unconditional bases of compactly supported matrix valued wavelets. Numerical Functional Analysis and Optimization, 22 (1&2): 223-253, 2001.

Peer-reviewed conferences

  1. S. An and K. Slavakis. Tensor-based binary graph encoding for variational quantum classifiers. To be presented at the IEEE International Conference on Quantum Communications, Networking, and Computing (QCNC), Nara, Japan, March 31 - April 2, 2025. [arXiv]

  2. D. T. Nguyen and K. Slavakis. Multilinear kernel regression and imputation via manifold learning: The dynamic MRI case. In IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), pp. 9466-9470, Seoul, Korea, 14-19 April, 2024.

  3. Y. Akiyama and K. Slavakis. Proximal Bellman mappings for reinforcement learning and their application to robust adaptive filtering. In IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), pp. 5855-5859, Seoul, Korea, 14-19 April, 2024.

  4. M. Vu, Y. Akiyama, and K. Slavakis. Dynamic selection of p-norm in linear adaptive filtering via online kernel-based reinforcement learning. In IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), pp. 1-5, Rhodes: Greece, June 4-10, 2023.

  5. Y. Chen, K. Okubo, K. Slavakis, and Y. Kitamoto. A machine-learning-based analysis method of AC magnetization spectra for estimating cluster distribution of magnetic nanoparticles. In IEEE International Magnetics Conference (INTERMAG), Sendai: Japan, May 2023.

  6. C. Ye, K. Slavakis, J. Nakuci, S. F. Muldoon, and J. Medaglia. Online classification of dynamic multilayer-network time series in Riemannian manifolds. In IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), pp. 3815-3819, Toronto: Canada, June 6-11, 2021.

  7. K. Slavakis and M. Yukawa. Outlier-robust kernel hierarchical-optimization RLS on a budget with affine constraints. In Proc. of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), pp. 5335-5339, Toronto: Canada, June 6-11, 2021.

  8. G. Shetty, K. Slavakis, U. Nakarmi, G. Scutari, and L. Ying. Kernel bi-linear modeling for reconstructing data on manifolds: The dynamic-MRI case. In Proc. of the 2020 European Signal Processing Conference (EUSIPCO), pp. 1482-1486, Amsterdam: The Netherlands, January 2021.

  9. C. Ye, K. Slavakis, S. Muldoon, J. Nakuci and J. Medaglia. Fast sequential multilayer brain-network state clustering. Presented at the Northeast Regional Conference on Complex Systems (NERCCS), Buffalo: NY: USA, April 1-3, 2020.

  10. K. Slavakis. Stochastic composite convex minimization with affine constraints. In Proc. of the Asilomar Conference on Signals, Systems and Computers, Pacific Grove, California, pp. 1871-1875, Oct. 28-31, 2018.

  11. U. Nakarmi, K. Slavakis, H. Li, C. Zhang, P. Huang, S. Gaire, and L. Ying. MLS: Self-learned joint manifold geometry and sparsity aware framework for highly accelerated cardiac cine imaging. In Proc. of the joint annual meeting ISMRM-ESMRMB, Paris: France, June 16-21, 2018.

  12. K. Slavakis, A. Konar, and N. Sidiropoulos. Fast projection-based solvers for the non-convex quadratically constrained feasibility problem. In Proc. of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary: Alberta: Canada, April 15-20, 2018.

  13. U. Nakarmi, K. Slavakis, and L. Ying. MLS: Joint manifold-learning and sparsity-aware framework for highly accelerated dynamic magnetic resonance imaging. In Proc. of the IEEE International Symposium on Biomedical Imaging (ISBI), Washington DC: USA, April 4-7, 2018.

  14. K. Slavakis, G. N. Shetty, A. Bose, U. Nakarmi and L. Ying. Bi-linear modeling of manifold-data geometry for dynamic-MRI recovery. In Proc. of the IEEE International Workshop on Computational Advances in Multi-Sensor Adaptive Processing (CAMSAP), Curacao: Dutch Antilles, Dec. 10-13, 2017.

  15. K. Slavakis, S. Salsabilian, D. S. Wack, S. F. Muldoon, H. Baidoo-Williams, J. Vettel, M. Cieslak and S. Grafton. Riemannian multi-manifold modeling and clustering in brain networks. In Proc. of SPIE Optics + Photonics, San Diego: California: USA, 6-10 Aug., 2017.

  16. U. Nakarmi, K. Slavakis, J. Lyu, C. Zhang and L. Ying. Beyond low-rank and sparsity: A manifold driven framework for highly accelerated dynamic magnetic resonance imaging. In Proc. of the International Society for Magnetic Resonance in Medicine (ISMRM) Meeting, Honolulu: USA, 22-27 April, 2017.

  17. U. Nakarmi, K. Slavakis, J. Lyu and L. Ying. M-MRI: A manifold-based framework to highly accelerated dynamic magnetic resonance imaging. In Proc. of the International Symposium on Biomedical Imaging (ISBI), Melbourne: Australia, 18-21 April, 2017.

  18. K. Slavakis, I. Yamada and S. Ono. Accelerating the hybrid steepest descent method for affinely constrained convex composite minimization tasks. In Proc. of ICASSP, New Orleans: USA, Mar. 5-9, 2017.

  19. K. Slavakis, S. Salsabilian, D. S. Wack, and S. F. Muldoon, H. Baidoo-Williams, J. Vettel, M. Cieslak, S. Grafton. Clustering brain-network-connectivity states using kernel partial correlations. In Proc. of the 50th Asilomar Conference on Signals, Systems and Computers, Pacific Grove, California, Nov. 6-9, 2016.

  20. K. Slavakis and I. Yamada. Accelerated hybrid steepest descent method for solving affinely constrained convex composite optimization problems. Presented at the International Conference on Continuous Optimization (ICCOPT), Tokyo: Japan, Aug. 6-11, 2016.

  21. K. Slavakis, S. Salsabilian, D. S. Wack, and S. F. Muldoon. Clustering time-varying connectivity networks by Riemannian geometry: The brain-network case. In Proc. of Statistical Signal Processing (SSP), Palma de Mallorca: Spain, June 26-29, 2016.

  22. U. Nakarmi, Y. Zhou, J. Lyu, K. Slavakis, and L. Ying. Accelerating dynamic magnetic resonance imaging by nonlinear sparse coding. In Proc. of ISBI, Prague: Czech Republic, April 13-16, 2016.

  23. G. V. Karanikolas, G. B. Giannakis, K. Slavakis, and R. M. Leahy. Multi-kernel based nonlinear models for connectivity identification of brain networks. In Proc. of ICASSP, Shanghai: China, Mar. 25-30, 2016.

  24. P. A. Traganitis, K. Slavakis, and G. B. Giannakis. Large-scale subspace clustering using random sketching and validation. In Proc. of the Asilomar Conference on Signals, Systems, and Computers, Nov. 8-11, 2015.

  25. X. Wang, K. Slavakis, and G. Lerman. Multi-manifold modeling in non-Euclidean spaces. In Proc. of the International Conference on Artificial Intelligence and Statistics (AISTATS), PMLR 38:1023-1032, 2015.

  26. P. A. Traganitis, K. Slavakis, and G. B. Giannakis. Spectral clustering of large-scale communities via random sketching and validation. Presented at the Conference on Information Systems and Sciences (CISS), Baltimore, Maryland, Mar. 18-20, 2015.

  27. P. A. Traganitis, K. Slavakis, and G. B. Giannakis. Clustering high-dimensional data via random sampling and consensus. Presented at GlobalSIP, Dec. 3-5, Atlanta: USA, 2014.

  28. P. A. Traganitis, K. Slavakis, and G. B. Giannakis. Big data clustering using random sampling and consensus. Presented at the Asilomar Conference on Signals, Systems, and Computers, Nov. 2-5, 2014.

  29. K. Slavakis, X. Wang, and G. Lerman. Clustering high-dimensional dynamical systems on low-rank matrix manifolds. Presented at the Asilomar Conference on Signals, Systems, and Computers, Nov. 2-5, 2014.

  30. M. Mardani, L. Ying, G. Scutari, K. Slavakis, and G. B. Giannakis. Dynamic MRI using subspace tensor tracking. In Proc. of the Engineering in Medicine and Biology Conference (EMBC), Aug. 26-30, Chicago, 2014.

  31. K. Slavakis and G. B. Giannakis. Online dictionary learning from big data using accelerated stochastic approximation algorithms. In ICASSP, Florence: Italy, May 4-9, 2014 (Special session: "Signal processing for big data").

  32. M. Zamanighomi, Z. Wang, K. Slavakis, and G. B. Giannakis. Linear minimum mean-square error estimation based on high-dimensional data with missing values. In 48th Annual Conference on Information Sciences and Systems (CISS), Princeton University: USA, Mar. 19-21, 2014.

  33. K. Slavakis, Y. Kopsinis, S. Theodoridis. New operators for fixed-point theory: The sparsity-aware learning case. In EUSIPCO (special session "Advances in set theoretic estimation and convex analysis for machine learning and signal processing tasks"), Marrakech: Morocco, Sept. 9-13, 2013.

  34. K. Slavakis, Y. Kopsinis, S. Theodoridis, G. B. Giannakis, and V. Kekatos. Generalized iterative thresholding for sparsity-aware online Volterra system identification. In International Symposium on Wireless Communication Systems (ISWCS), Ilmenau: Germany, Aug. 27-30, 2013.

  35. S. Theodoridis, Y. Kopsinis, K. Slavakis, and S. Chouvardas. Sparsity-aware adaptive learning: A set theoretic estimation approach. In IFAC International Workshop on Adaptation and Learning in Control and Signal Processing (ALCOSP), Caen: France, July 3-5, 2013, (plenary paper)</font>.

  36. K. Slavakis, G. Leus, and G. B. Giannakis. Online robust portfolio risk management using total least-squares and parallel splitting algorithms. In Proc. of ICASSP, Vancouver: Canada, May 26-31, 2013.

  37. Y. Kopsinis, K. Slavakis, S. Theodoridis, and S. McLaughlin. Thresholding-based sparsity-promoting online algorithms of low complexity. In Proc. of ISCAS, Beijing, China, May 19-23, 2013.

  38. K. Slavakis, G. B. Giannakis, and G. Leus. Robust sparse embedding and reconstruction via dictionary learning. In Proc. of 47th Annual Conference on Information Sciences and Systems (CISS), Johns Hopkins University: Baltimore: USA, Mar. 20-22, 2013.

  39. K. Slavakis, G. B. Giannakis, and G. Leus. Nonlinear embedding and reconstruction via locally affine dictionary learning. Information Theory and Applications (ITA) Workshop, San Diego: USA, Feb. 10-15, 2013.

  40. S. Chouvardas, K. Slavakis, Y. Kopsinis, and S. Theodoridis. Sparsity-promoting adaptive algorithm for distributed learning in diffusion networks. In Proceedings of the European Signal Processing Conference (EUSIPCO), Bucharest: Romania, Aug. 27-31, 2012.

  41. Y. Kopsinis, K. Slavakis, S. Theodoridis, and S. McLaughlin. Generalized thresholding sparsity-aware algorithm for low complexity online learning. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP), pp. 3277-3280, Kyoto: Japan, March 25-30, 2012.

  42. K. Slavakis, Y. Kopsinis, and S. Theodoridis. Robust adaptive sparse system identification by using weighted l1 balls and Moreau envelopes. In Proceedings of the European Signal Processing Conference (EUSIPCO), Barcelona: Spain, Aug. 29 - Sept. 2, 2011, (presented in the Special Session "Sparsity aware processing: theory and applications").

  43. Y. Kopsinis, K. Slavakis, S. Theodoridis, and S. McLaughlin. Reduced complexity online sparse signal reconstruction using projections onto weighted l1 balls. In Proceedings of the International Conference on Digital Signal Processing (DSP), Special Session "Sparsity-aware signal processing", Corfu: Greece, July 6-8, 2011, (Invited).

  44. K. Slavakis, Y. Kopsinis, and S. Theodoridis. Revisiting adaptive least-squares estimation and application to online sparse signal recovery. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP), pp. 4292-4295, Prague: Czech Republic, May 22-27, 2011.

  45. S. Chouvardas, K. Slavakis, and S. Theodoridis. Trading off communications bandwidth with accuracy in adaptive diffusion networks. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP), pp. 2048-2051, Prague: Czech Republic, May 22-27, 2011.

  46. K. Slavakis, S. Theodoridis, and I. Yamada. Low complexity projection-based adaptive algorithm for sparse system identification and signal reconstruction. In Proceedings of the Asilomar Conference on Signals, Systems, and Computers, Pacific Grove: California: USA, November 7-10, 2010, (Invited).

  47. P. Bouboulis, K. Slavakis, and S. Theodoridis. Edge preserving image denoising in reproducing kernel Hilbert spaces. In Proceedings of the IAPR International Conference on Pattern Recognition (ICPR), pp. 2660-2663, Istanbul: Turkey, August 23-26, 2010 (best-paper award, track III: Signal, speech, image and video processing).

  48. S. Chouvardas, K. Slavakis, and S. Theodoridis. A novel adaptive algorithm for diffusion networks using projections onto hyperslabs. In Proceedings of the IAPR Workshop on Cognitive Information Processing (CIP), pp. 393-398, Italy, June 14-16, 2010 (best-student-paper award).

  49. K. Slavakis, Y. Kopsinis, and S. Theodoridis. Adaptive algorithm for sparse system identification using projections onto weighted l1 balls. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP), pp. 3742-3745, Dallas: Texas: USA, March 14-19, 2010.

  50. M. Yukawa, K. Slavakis, and I. Yamada. Multi-domain adaptive filtering by feasibility splitting. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP), Dallas: Texas: USA, March 14-19, 2010.

  51. M. Yukawa, K. Slavakis, and I. Yamada. Signal processing in dual domain by adaptive projected subgradient method. In Proceedings of the International Conference on Digital Signal Processing (DSP), Santorini: Greece, July 5-7, 2009.

  52. K. Slavakis, P. Bouboulis, and S. Theodoridis. Online kernel receiver for multiaccess MIMO channels. In Proceedings of the IEEE International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), pp. 221-224, Perugia: Italy, June 21-24, 2009.

  53. K. Slavakis and S. Theodoridis. Affinely constrained online learning and its application to beamforming. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP), pp. 1573-1576, Taipei, April 19-24, 2009.

  54. K. Slavakis, S. Theodoridis, and I. Yamada. Constrained adaptive learning in reproducing kernel Hilbert spaces: the beamforming paradigm. In Proceedings of the IEEE Machine Learning for Signal Processing (MLSP) Workshop, pp. 32-37, Cancun: Mexico, October 16-19, 2008.

  55. K. Slavakis, S. Theodoridis, and I. Yamada. Robust adaptive nonlinear beamforming by kernels and projection mappings. In Proceedings of EUSIPCO, Lausanne: Switzerland, August 25-29, 2008.

  56. K. Slavakis and S. Theodoridis. Optimal sliding window sparsification for online kernel-based classification by projections. In Proceedings of the IAPR Cognitive Information Processing (CIP) Workshop, Santorini: Greece, pp. 30-35, June 2008.

  57. K. Slavakis and S. Theodoridis. Sliding window online kernel-based classification by projection mappings. In Proceedings of the IEEE ISCAS, Seattle: USA, pp. 49-52, May 2008.

  58. F. Fourli-Kartsouni, K. Slavakis, G. Kouroupetroglou, and S. Theodoridis. A Bayesian network approach to semantic labelling of text formatting in XML corpora of documents. Lecture Notes in Computer Science (LNCS), Vol. 4556, pp. 299-308, 2007.

  59. K. Slavakis, S. Theodoridis, and I. Yamada. Online sparse kernel-based classification by projections. In Proceedings of the IEEE Machine Learning for Signal Processing (MLSP), Thessaloniki: Greece, pp. 294-299, August 2007.

  60. K. Slavakis, S. Theodoridis, and I. Yamada. Online kernel-based classification by projections. In Proceedings of the IEEE ICASSP, Hawaii: USA, vol. II, pp. 425-428, April 2007.

  61. I. Yamada, K. Slavakis, M. Yukawa, and R. Cavalcante. The adaptive projected subgradient method and its applications to signal processing problems. In Proceedings of the IEEE ISCAS (Invited), Kos: Greece, May 2006.

  62. K. Slavakis, M. Yukawa, and I. Yamada. Robust Capon beamforming by the adaptive projected subgradient method. In Proceedings of the IEEE ICASSP, Toulouse: France, pp. 1005-1008, May 2006.

  63. M. Yukawa, K. Slavakis, and I. Yamada. Stereo echo canceler by adaptive projected subgradient method with multiple room-acoustics information. In Proceedings of the IWAENC, S03-15, pp. 185-188, Eindhoven: The Netherlands, September 2005.

  64. K. Slavakis, I. Yamada, N. Ogura, and M. Yukawa. Adaptive projected subgradient method and set theoretic adaptive filtering with multiple convex constraints. In Proceedings of the 38th Asilomar Conference on Signals, Systems, and Computers, November 2004.

  65. K. Slavakis, I. Yamada, and K. Sakaniwa. Spectrum estimation of real vector wide sense stationary processes by the hybrid steepest descent method. In Proceedings of the IEEE ICASSP, Orlando: USA, May 2002.

  66. I. Yamada, K. Slavakis, and K. Yamada. An efficient robust adaptive filtering scheme based on parallel subgradient projection techniques. In Proceedings of the IEEE ICASSP, Salt Lake City: USA, May 2001.

  67. K. Slavakis and I. Yamada. Compactly supported matrix valued wavelets-Biorthogonal unconditional bases. In Proceedings of the IEEE ISCAS (Invited: Special Session), Sydney: Australia, May 2001.

  68. K. Slavakis and I. Yamada. Biorthogonal bases of compactly supported matrix valued wavelets. In Proceedings of the IEEE ISSPA, volume 2, pp. 981-984, Brisbane: Australia, August 1999.

Non-peer-reviewed conferences

  1. D. T. Nguyen and K. Slavakis. Multi-linear kernel regression and imputation in data manifolds. Signal Processing (SIP) Symposium, Kyoto: Japan, November 6-8, 2023.

  2. Y. Akiyama and K. Slavakis. Distributed reinforcement learning via proximal Bellman mappings. Signal Processing (SIP) Symposium, Kyoto: Japan, November 6-8, 2023.

  3. Y. Akiyama and K. Slavakis. Proximal Bellman mappings for robust adaptive filtering. Signal Processing (SIP) Symposium, Kyoto: Japan, November 6-8, 2023.

  4. Y. Akiyama, M. Vu, and K. Slavakis. Online lightweight reinforcement learning against outliers in linear adaptive filtering. Signal Processing (SIP) Symposium, Niigata: Japan, December 13-15, 2022.

  5. M. Vu, Y. Akiyama, and K. Slavakis. Least-mean p-norm adaptive filtering via reinforcement learning. Signal Processing (SIP) Symposium, Niigata: Japan, December 13-15, 2022.

Book Chapters

  1. K. Slavakis, P. Bouboulis, and S. Theodoridis. Online learning in reproducing kernel Hilbert spaces. In Academic Press Library in Signal Processing: Volume 1 Signal Processing Theory and Machine Learning, vol. 1, ch. 17, pp. 883-987, Elsevier, 2014.

  2. S. Theodoridis, Y. Kopsinis, and K. Slavakis. Sparsity-aware learning and compressed sensing: An overview. In Academic Press Library in Signal Processing: Volume 1 Signal Processing Theory and Machine Learning, vol. 1, ch. 23, pp. 1271-1377, Elsevier, 2014. [arXiv]

Tutorials

  1. K. Slavakis. Learning from data in manifolds: Methods, applications, and recent developments. Signal Processing (SIP) Symposium, Tokyo Institute of Technology: Tokyo: Japan, November 9-12, 2021.

  2. G. B. Giannakis, K. Slavakis, and G. Mateos. Signal processing tools for big data analytics. EUSIPCO, Nice: France, Aug. 31 - Sept. 4, 2015.

  3. G. B. Giannakis, K. Slavakis, and G. Mateos. Signal processing tools for big data analysis. IEEE ICASSP, Brisbane: Australia, April 19-20, 2015.

  4. G. B. Giannakis, K. Slavakis, and G. Mateos. Signal processing for big data. EUSIPCO, Lisbon: Portugal, Sept. 1, 2014.

  5. G. B. Giannakis, K. Slavakis, and G. Mateos. Signal processing for big data. IEEE ICASSP, Florence: Italy, May 5, 2014.

  6. S. Theodoridis, Y. Kopsinis, K. Slavakis, and S. Chouvardas. Sparsity-aware adaptive learning: A set theoretic estimation approach. IFAC International Workshop on Adaptation and Learning in Control and Signal Processing (ALCOSP), Caen: France, July 3-5, 2013.

  7. S. Theodoridis, I. Yamada, and K. Slavakis. Learning in the context of set theoretic estimation: An efficient and unifying framework for adaptive machine learning and signal processing. IEEE ICASSP, Kyoto: Japan, March 25-30, 2012, (the slides can be found here).

Preprints and Technical Reports

  1. Y. Akiyama, M. Vu, and K. Slavakis. Online and lightweight kernel-based approximate policy iteration for dynamic p-norm linear adaptive filtering. 2022. [arXiv] [TechRxiv]

  2. X. Wang, K. Slavakis, and G. Lerman. Riemannian multi-manifold modeling. 2014. [arXiv]